“May we not call them the ghosts of departed quantities?”—George Berkeley
Last week I promised you a lighthearted article on nonexistent (imaginary) numbers, and I’m sure that you’ve all been on the edge of your seats in anticipation. However, it has since occurred to me that a few of you aren’t fans of math. I’ve even heard that some are intimidated by it – almost phobic in some cases. As hard as I find this to believe, I’ll do my best to alleviate your fears. On the other hand, my apologies to those of you for whom some of this will be remedial. Then again, you might not know as much as you think you do. Here goes.
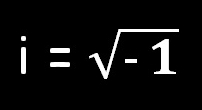 The first thing that you should know about imaginary numbers is that they’re imaginary. That’s why they’re called that. They don’t exist. Mathematicians can give you an explanation as to why they’re valid, but they have to preface this by saying that all numbers are only abstract concepts anyway. Try telling that to your kids when there are three of them and only two popsicles. Nice try mathematicians. The truth is that most mathematical equations do explain something that we can all wrap our heads around, even if the formula itself is beyond our comprehension. Even calculus is, more or less, just a way of computing the area under a curve. That’s not too hard to visualize. So where did we get these numbers that even mathematicians call imaginary?*
The first thing that you should know about imaginary numbers is that they’re imaginary. That’s why they’re called that. They don’t exist. Mathematicians can give you an explanation as to why they’re valid, but they have to preface this by saying that all numbers are only abstract concepts anyway. Try telling that to your kids when there are three of them and only two popsicles. Nice try mathematicians. The truth is that most mathematical equations do explain something that we can all wrap our heads around, even if the formula itself is beyond our comprehension. Even calculus is, more or less, just a way of computing the area under a curve. That’s not too hard to visualize. So where did we get these numbers that even mathematicians call imaginary?*
It all started with squares and square roots. I’m sure that you all know that a square is a number times itself: 2 х 2 = 22 = 4, 3 х 3 = 32 = 9, etc. Conversely, the square root of 4 is 2, and the square root of 9 is 3 for the very same reason, but the other way around. Simple enough, until you consider negative numbers. For instance, the square root of -4 can’t be 2 or -2 because 2 х 2 and -2 х -2 are both positive 4. (In multiplication, two negatives equals a positive in case you’ve forgotten. It was probably never adequately explained to you why this is so, but that’s another story. The failure of most teachers to really show their students why things work and what is happening with the numbers is probably one of the reasons so many are intimidated by math, but that’s also outside the scope of our current topic.) It also can’t be 2 х -2 because those are different numbers. You can’t say that 2 and -2 are both the square roots of -4 because that violates the definition of a root. You also can’t say that negative numbers have no square root just because you can’t figure out what they are. That’s numerical discrimination.
Enter Gerolamo Cardano, an Italian mathematician in the 16th century who decided to fix this problem by using the letter i to represent the square root of -1. No one really knew what i was, but at least they now had something to call it. Furthermore, since 1 is the square root of 1 (12 = 1), and multiplying anything times 1 gives you the same number that you started with (1 х 23 = 23), and i is the square root of -1, you could now define the square root of any negative number by multiplying it by i, e.g., the square roots of -4 and -25 are 2i and 5i respectively. Problem solved…sort of. Remember, they still didn’t really know what i meant. Just having something to call it didn’t really explain anything.
Here’s the real problem. You can count all of the apples on a tree and we all know what the final tally means, although there must be better hobbies. You can mark the point 2.35817 on a number line if you have a big enough line or a sharp enough pencil. You can even plot negative numbers on a line, but you can’t point to any place, not even on a three-dimensional grid, and say that this is where an imaginary number is located. It seems almost as if they exist in another dimension(?).
So who cares? It’s just some weird math thing that some geeky Italian came up with nearly 600 years ago. So what if it doesn’t have anything to do with the real world?
That was a fair question for over 300 years, but then scientists started finding multiple systems in the real world that can only be described mathematically using these apparently unreal numbers. For instance, you need them to explain some electrical systems, Einstein’s theory of relativity, quantum mechanics and computer technology. The list goes on and on.
Just for fun, take a look at this unintimidating little equation and watch where it takes us.
5x2 + 5 = 0
5x2 + 5 – 5 = 0 – 5
5x2 = -5
5x2/5 = -5/5
X2 = -1 or i
There’s really nothing too complex about any of this, except the answer. My point being that imaginary numbers don’t just pop up in hyper-complex equations that most of us couldn’t decipher if our lives depended on it. It sneaks its way into seemingly simple places as well.
Before we go any further, it would helpful to know the difference between pure and applied math. It’s pretty simple, really. Pure math is math that works, but nobody knows what it means. It has no practical application, at least for now. That’s where imaginary numbers lived for centuries, and so no one had to take them seriously. Applied math is math that serves a purpose. We can use it to explain the world we live in.
For example, at some point thousands of years ago, Zug was doodling in the dirt with a stick in his cave when he figured out that if he drew two vertical lines, and then drew two horizontal lines across these, his lines intersected each other at four points (#). From this he deduced something that he decided to call 2 + 2 = 4, and that was pure math because he didn’t know what to do with it at the time. Zug told his friend Og about this, but Og not impressed. Og not even know what Zug grunting about. Og only have one mouth, one head, two arm and two leg. What is four? Og not have four of anything. Four make no sense to Og.
But then one day Og realized that he had two mastodon bones when his friend Gor stopped by and gave him two more mastodon bones that he wasn’t using. Bright light go on over Og’s head. Him had one mastodon bone for each hand in next fight with forest people, but now him have more mastodon bone than hand. This better. Now if break bone in fight, him have other bone to club forest person with. Where he might carry them is a mystery, but you get the idea. The point is, suddenly 2 + 2 = 4 has  meaning – an understood application. Zug came up with the equation, but Og figured out how it related to a situation in the real world, and so then it became applied math.
meaning – an understood application. Zug came up with the equation, but Og figured out how it related to a situation in the real world, and so then it became applied math.
As you might have guessed, this is an oversimplification and not entirely accurate, but you get the point. And yeah, I know. Og have ten finger and ten toe, so how him not know about four? Work with me here. You don’t actually believe that this really happened, do you?
Of course, pure math doesn’t just magically become applied math because somebody found a use for it. The use was always there, it just took someone a while to find out what it was. It can also go the other way around. Sometimes scientists come up with some great ideas, but they can’t prove them because the equation that would confirm their idea has yet to be discovered. That’s why physicists spend so much time screwing around with math even though they aren’t mathematicians.
A good illustration of this is that things have always fallen to the ground at 32 feet per second squared. Isaac Newton didn’t invent gravity, he just came up with the math that explains how it works…at least to some extent.** And Og knew that having four bones to fight the forest people with was better than just two, but he didn’t have the equation to prove it with until Zug came up with 2 + 2 = 4. That Zug was a freakin genius, although the whole “bow and arrow” thing and “time only illusion created by spongy thing inside of head” that he kept babbling on about were just stupid.
From these humble beginnings in Zug’s cave, humans went on to discover multiplication and division and fractions and algebra and geometry and, later on, the even more advanced forms of mathematics that scare the flaming green monkey crap out of English lit and art history majors, many of which won’t work without the arcane square root of -1 as represented by the insidious i.
Occultist and scientific philosopher (among other things) Robert Anton Wilson was fascinated by these numbers that don’t exist anywhere in the “real” world and yet somehow cannot be removed from it. He wrote of a mystical experience that he had in high school in Cosmic Trigger: Volume II involving an experiment with an oscilloscope. In the experiment, he placed a piece of paper on the oscilloscope and traced the wave form of a voltage in an alternating current. He then drew a picture of the wave form as predicted by the equation which describes this experiment, which included the mysterious square root of -1, and found that they were identical. While most kids would just be happy that they got the right answer, Wilson was always a bit of a deeper thinker. He was amazed at how the seemingly unreal world of math could so accurately describe the reality that we experience as the everyday world. Wilson assures us that this connection has never been adequately explained but has nevertheless gotten both stronger and more bizarre over the last century.
On the other hand, science has been increasingly informing us over this same period that what we perceive as the “real world” is the actual illusion. Solid matter is, in reality, mostly empty space. It’s composed of atoms that have neither color nor temperature. Light is both a particle and a wave. Depending on what sort of observation you’re making, it will magnanimously behave as whichever one you like. Even time has been proven to be a relative concept (at best), just as Einstein predicted, so Zug was really onto something there. He really was a man ahead of his (perhaps illusory) time.
So that’s the world we live in. As if big hairy monsters and little gray aliens and ghosts and all of the other paranormal oddities weren’t bad enough, now we have to deal with the fact that even math and science tell us that our universe is crazier than a dancing mouse. Supposedly, what we experience as the everyday world doesn’t really exist at all, but these numbers that we call imaginary do. Time may not be real, but the square root of -1 is.
Still, these unreal numbers must be real on some level, otherwise televisions and microwave ovens would explode and send shards of glass and plastic flying through our kitchens and living rooms all the time, and the electronic systems on airplanes would suddenly malfunction for no good reason and send planes plummeting to the ground on a regular basis. Since these things rarely happen, it would seem that these nonexistent numbers must exist somewhere, even if only in our heads(!?!).
That’s a bit disconcerting, but also intriguing – sort of like getting on a 747 and finding out that your pilot, copilot and navigator are Superman, Peter Pan and Puff the Magic Dragon. You know they aren’t real, but if you can’t trust those guys to make this thing fly, who can you trust? Even so, flying  seven miles in the air in a craft that you know is kept aloft at least in part by something that seems to exist only in some bizarre, mathematical netherworld does take a bit of a leap of faith. Luckily for me, I tend to think that the other dimensions that these numbers might reside in do exist and probably have a greater impact on our own than is currently known. The again, I could be completely wrong. So buckle your seat belt…if you think that will help.
seven miles in the air in a craft that you know is kept aloft at least in part by something that seems to exist only in some bizarre, mathematical netherworld does take a bit of a leap of faith. Luckily for me, I tend to think that the other dimensions that these numbers might reside in do exist and probably have a greater impact on our own than is currently known. The again, I could be completely wrong. So buckle your seat belt…if you think that will help.
_______________________________________________________________________
*This name was originally given to them as a way of mocking the idea of their existence, but it stuck.
**Nobody really knows how gravity works to this day. We can describe its effects mathematically with quite a bit of accuracy, but we don’t know how or why it works.


